1.1 Problembeschreibung
Angenommen wird ein Szenario, in dem Fluid zwischen zwei koaxialen Zylindern eingeschlossen ist, die mathematisch betrachtet als unendlich lang angesehen werden können. In der Praxis weisen diese jedoch meist eine endliche Länge auf. Diese mathematische Annäherung erlaubt es, den zweidimensionalen Fall zu modellieren, ohne zunächst die Einflüsse der Randbedingungen zu berücksichtigen.
Das betrachtete Fluid ist inkompressibel und newtonisch, und die Strömung wird als laminar angenommen. Die Zylinder rotieren jeweils mit einer individuellen Winkelgeschwindigkeit Ω1 beziehungsweise Ω2. Die Radien der Zylinder werden mit R1 und R2 bezeichnet, wobei die Z-Achse die koaxiale Zylinderachse darstellt.
In der Literatur ist die entstehende Fluidbewegung als Couette-Strömung bekannt, eine spezielle Form der Strömung zwischen rotierenden Zylindern. Die Untersuchung dieses Phänomens ermöglicht Einblicke in die komplexen Strömungsverhältnisse und ist von Interesse für verschiedenste Anwendungen in den Bereichen der Strömungsmechanik, Ingenieurwissenschaften und Physik.
1.2 Analytische Lösung
Die analytische Lösung basiert auf der Lösung der Navier-Stokes-Gleichungen für inkompressible Fluide. Dabei erweist es sich als vorteilhaft, die vorliegende Geometrie unter Verwendung von Zylinderkoordinaten zu betrachten, was die Berechnungen vereinfacht und die Symmetrie des Problems ausnutzt.
Diese Zusammenhänge erleichtern die analytische Berechnung der Navier-Stokes-Gleichungen und bilden somit die Grundlage für die Entwicklung von Lösungsansätzen zur Bewältigung der Strömungsproblematik zwischen den Zylindern.
Auf die gleiche Weise, wie die Geschwindigkeit eines festen Körpers durch das Lösen von Newtons zweitem Gesetz berechnet werden kann,
kann die Geschwindigkeit eines Fluids (Flüssigkeit oder Gas) durch das Lösen der Navier-Stokes-Gleichungen berechnet werden.
Die Navier-Stokes-Gleichungen sind analog zu Newtons zweitem Gesetz und besagen, dass die Änderungsrate des Impulses eines Fluids gleich der Summe der externen Kräfte ist, die auf das Fluid wirken. Allerdings werden die Navier-Stokes-Gleichungen auf ein endliches Volumen von Fluid angewendet, anstatt auf einen festen Körper.
In der Literatur ist oft folgende allgemeine Schreibweise der Gleichungen zu finden:
- Radiale Impulsgleichung:$$r:\rho\left(\frac{\partial u_r}{\partial t}+u_r\frac{\partial u_r}{\partial r}+\frac{u_\varphi}{r}\frac{\partial u_r}{\partial\varphi}-\frac{u_\varphi^2}{r}+u_z\frac{\partial u_r}{\partial z}\right)=-\frac{\partial p}{\partial r}+\mu\left(\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u_r}{\partial r}\right)+\frac{1}{r^2}\frac{\partial^2u_r}{\partial\varphi^2}+\frac{\partial^2u_r}{\partial z^2}-\frac{u_r}{r^2}-\frac{2}{r^2}\frac{\partial u_\varphi}{\partial\varphi}\right)+\frac{1}{3}\mu\left(\frac{1}{r}\frac{\partial}{\partial r}\left(ru_r\right)+\frac{1}{r}\frac{\partial u_\varphi}{\partial\varphi}+\frac{\partial u_z}{\partial z}\right)+\rho g_r$$
- Axiale Impulsgleichung: $$\varphi:\rho\left(\frac{\partial u_\varphi}{\partial t}+u_r\frac{\partial u_\varphi}{\partial r}+\frac{u_\varphi}{r}\frac{\partial u_\varphi}{\partial\varphi}+u_z\frac{\partial u_\varphi}{\partial z}-\frac{u_ru_\varphi}{r}\right)=-\frac{1}{r}\frac{\partial p}{\partial\varphi}+\mu\left(\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u_\varphi}{\partial r}\right)+\frac{1}{r^2}\frac{\partial^2u_\varphi}{\partial\varphi^2}+\frac{\partial^2u_\varphi}{\partial z^2}-\frac{u_\varphi}{r^2}-\frac{2}{r^2}\frac{\partial u_r}{\partial\varphi}\right)+\frac{1}{3}\mu r\left(\frac{1}{r}\frac{\partial}{\partial r}\left(ru_r\right)+\frac{1}{r}\frac{\partial u_\varphi}{\partial\varphi}+\frac{\partial u_z}{\partial z}\right)+\rho g_\varphi$$
- Azimutale Impulsgleichung: $$z:\rho\left(\frac{\partial u_z}{\partial t}+u_r\frac{\partial u_z}{\partial r}+\frac{u_\varphi}{r}\frac{\partial u_z}{\partial\varphi}+u_z\frac{\partial u_z}{\partial z}\right)=-\frac{\partial p}{\partial z}+\mu\left(\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u_z}{\partial r}\right)+\frac{1}{r^2}\frac{\partial^2u_z}{\partial\varphi^2}+\frac{\partial^2u_z}{\partial z^2}\right)+\frac{1}{3}\mu\left(\frac{1}{r}\frac{\partial}{\partial r}\left(ru_r\right)+\frac{1}{r}\frac{\partial u_\varphi}{\partial\varphi}+\frac{\partial u_z}{\partial z}\right)+\rho g_z$$
Die Gleichungen (1) und (2) können entkoppelt voneinander gelöst werden. Die zweite hat die Lösung vom Typ
Die Konstanten a und b können aus den Randbedingungen an Zylinderoberflächen gewonnen werden. Das Fluid bleibt an diesen aufgrund der sogenannten „no slip“ Bedingung haften und weist somit gleiche Geschwindigkeiten wie die Zylinder selbst auf:
Einsetzen der Konstanten ergibt die Geschwindigkeitsverteilung über den Umfang:
Um die Druckverteilung im Fluid zu erhalten, wird die Gleichung (3) in (1) eingesetzt:
Die Lösung dieser Differentialgleichung lässt durch die Separation der Variablen ermitteln:
Alle gesuchten Unbekannten sind nun ermittelt und wir können ein konkretes Beispiel mit Zahlenwerten untersuchen.
1.3 Konkretes Beispiel
- R1 = 70 mm,
- R2 = 100 mm
- Ω1 = 180 RPM $$ \approx\ $$18.85 rad/s
- Ω2 = -Ω1
- $$\rho$$ = 970 kg/m3 (Dichte bei Raumtemperatur)
- η = 0.0216019 kg/m/s (die dynamische Viskosität brauchen wir später für die Numerik)
1.4 Numerisches Modell
Es werden drei Berechnung mit unterschiedlichen Diskretisierungen durchgeführt:
- feines und strukturiertes Netz,
- mittelgrobes und strukturiertes Netz,
- grobes und unstrukturiertes Netz. Dabei wurden lediglich die „default“ Einstellungen vom Programm übernommen.
1.5 Analytik vs. Numerik
Wir widmen uns den Analysen des Systems. In der aktuellen Aufgabenstellung interessiert uns das Geschwindigkeitsfeld des Fluids und die dazugehörige Druckverteilung. Zusätzliche Fragestellungen wie die Temperaturverteilung oder kritische Rotationsgeschwindigkeiten können entsprechend ergänzend betrachtet werden. Je nach Analyse sind diese deutlich komplexer und müssen besonders behandelt werden.
1.5.1 Geschwindigkeit
Die Gleichung (3) beschreibt analytisch das Geschwindigkeitsfeld des Fluids. Nach dem Einsetzen der Werte lässt sich das Feld entsprechend grafisch darstellen. Da wir und nicht nur für die analytisch-geschlossene Lösung, sondern auch für die numerische Näherungslösung interessieren, lassen wir diese in verschiedenen Netzqualitäten darstellen. Zu besseren Abbildung der Ergebnisse, wird das Geschwindigkeitsfeld nicht in seinen Einzelkomponenten, sondern als Betrag gebildet. Dies eliminiert zwar jegliche Informationen über die Geschwindigkeitsrichtung auf den ersten Blick, stellt sich aber in der späteren Darstellung als nützlich heraus.
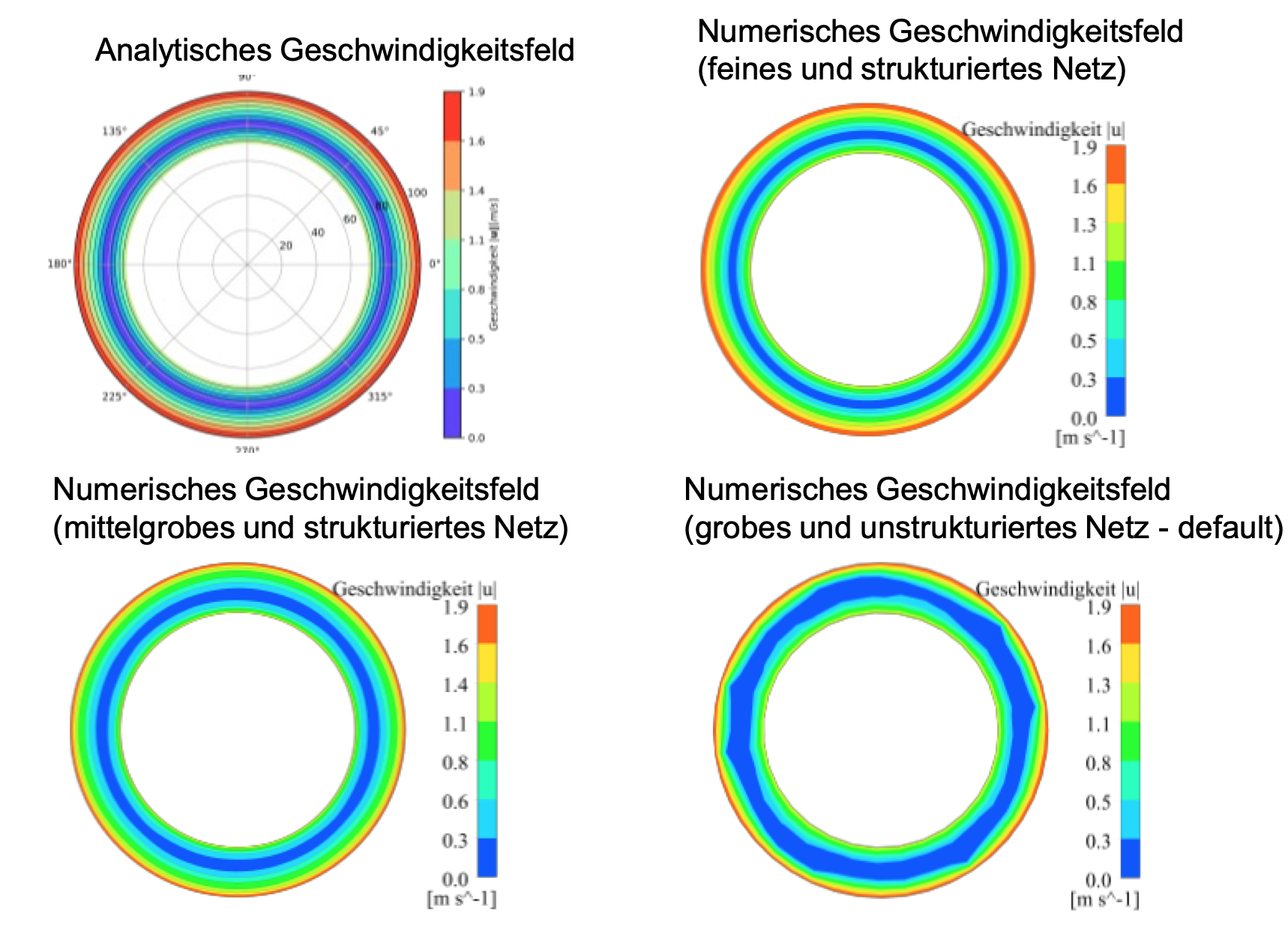
Analytische Lösung zeigt von Null verschiedene Geschwindigkeiten an den Oberflächen der Zylinder auf und einen Bereich dazwischen, wo die Geschwindigkeit tatsächlich den Wert Null annimmt. An dieser Stelle geschieht der Richtungswechsel der Geschwindigkeit. Die Erwartungen sind demnach erfüllt.
In der ersten oberflächlichen Betrachtung unterscheiden sich die Bilder nur schwach voneinander. Was ohne Mühe erkannt, werden kann, ist dass die Ergebnisse mit dem “default“ Netz lediglich unsanfter sind, aber im Großen und Ganzen die Analytik abbilden. Leider sind die numerisch erzeugten „farbigen Bilder“ allein nicht immer aussagekräftig und es werden an der Stelle Zahlenwerte benötigt, um einen seriösen Vergleich zwischen Analytik und Numerik herzustellen. Um die Ergebnisse detaillierter zu analysieren, wird durch das Fluid einen Pfad gelegt, der die physikalischen Eigenschaften im Fluid darstellt. Es wird die L2-Norm der Geschwindigkeit über den Radius (von Start des Pfades bei R1 bis zum Ende des Pfades bei R2) grafisch darstellt:
Die tangentialen Geschwindigkeiten des Fluids sollen erwartungsgemäß am Anfang und Ende des Plots den tangentialen Geschwindigkeiten der Zylinder bei R1 und R2 entsprechen:

Unsere Erwartungen sind vollständig erfüllt.
Wird sich nun den numerischen Ergebnissen der CFD-Analyse gewidmet, kann deutlicher erkannt werden, wie groß die Fehler der Simulation bei schlechten Netzen sind. Nur das gute und strukturierte Netz gibt ausreichend genau die analytischen Ergebnisse der Berechnung wieder.
1.5.2 Druck
Wie bei der Geschwindigkeitsverteilung wird nun das Geschwindigkeitsfeld ermittelt. Analytisch beschreibt Gleichung (4) die entsprechende Druckverteilung im Fluid. Unten werden die Verteilungen grafisch dargestellt.
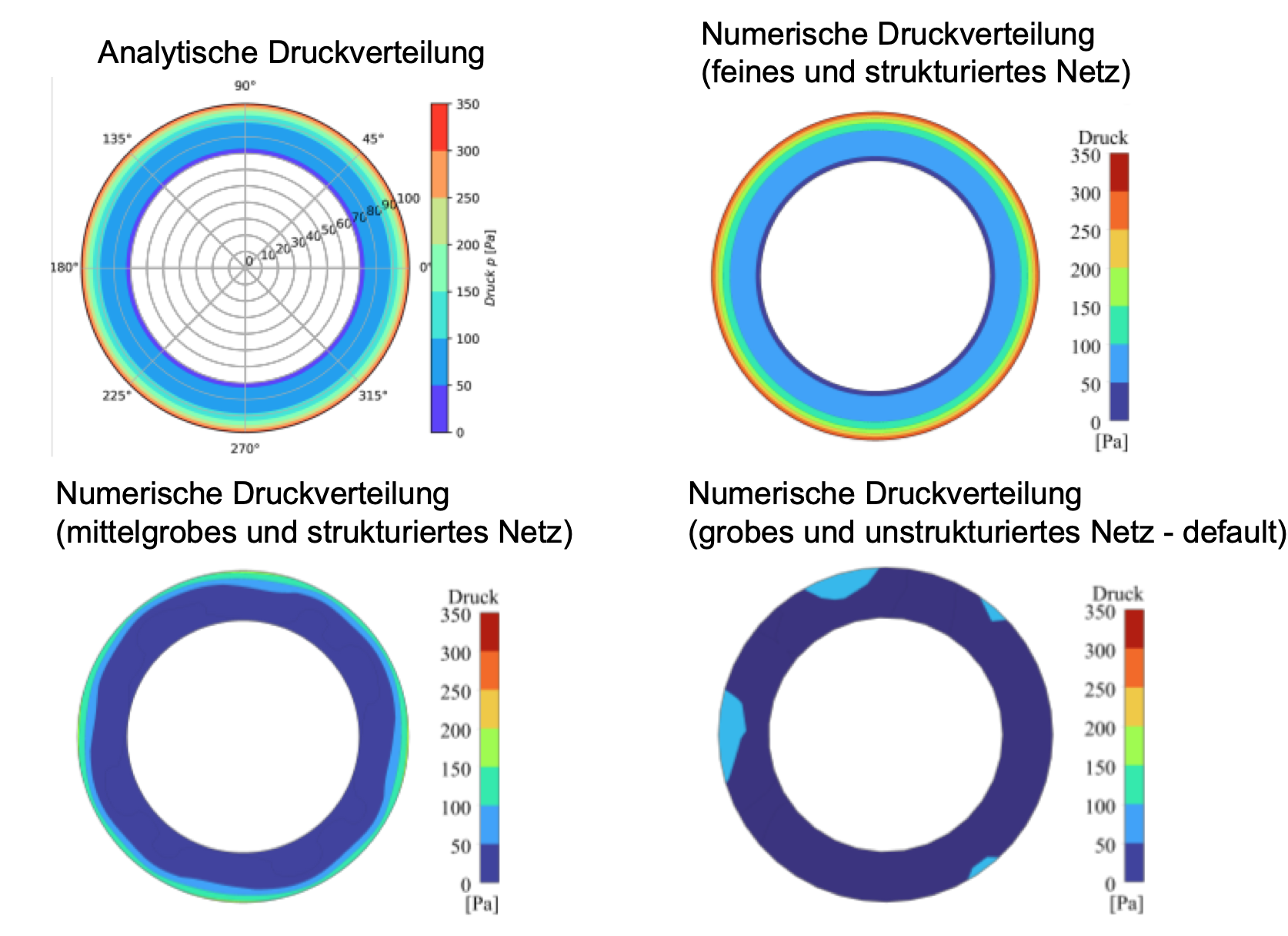
Die Abweichung der Numerik von der Analytik ist auch an diesen Abbildungen deutlich zu erkennen. Der Einfluss des Netzes ist viel größer als bei dem Geschwindigkeitsfeld.
Auch hier wird der Druck über den gleichen Pfad wie in der Geschwindigkeit ausgewertet:
Auch hier spielt die Netzqualität eine enorm wichtige Rolle bei den Ergebnissen und der Fehler bei schlechten Netzen ist größer als im Geschwindigkeitsfeld zu erkennen.
1.6 Fazit
Selbst bei vermeintlich simplen Problemen ist es erstaunlich einfach, in die Falle von Fehlern und Ungenauigkeiten zu treten und die resultierenden Berechnungen können von zweifelhafter Qualität sein. Die Validierung numerischer Modelle ist daher von entscheidender Bedeutung. Ohne eine solide Validierung, sei es durch analytische Methoden oder experimentelle Daten, besteht das Risiko wertlose bzw. falsche Ergebnisse zu liefern.
Besonders moderne Computational Fluid Dynamics (CFD)-Programme suggerieren oft eine beinahe mühelose Lösung von Strömungsproblemen. Mit ihren „default“ Einstellungen nehmen sie dem Anwender einen erheblichen Teil der Arbeit ab. Doch hier liegt eine potenzielle Gefahr: Das erzeugte Ergebnis ist zwar schnell verfügbar, jedoch nicht zwangsläufig korrekt. Oftmals weichen die Simulationsergebnisse erheblich von der Realität ab.
Dieses Phänomen wird besonders deutlich bei den vorliegenden simplen Studien in einem zweidimensionalen Raum mit inkompressiblen, stationären und laminaren Strömungsbedingungen. Obwohl die numerische Lösung auf den ersten Blick akzeptabel erscheint, können selbst bei scheinbar banalen Bedingungen Fehler auftreten, die das Ergebnis stark beeinträchtigen. Dies unterstreicht die Notwendigkeit, numerische Modelle sorgfältig zu validieren und die Grenzen ihrer Anwendbarkeit zu verstehen.
Wenn Sie sich selbst nicht als versierter Anwender der Numerik fühlen oder die analytischen Methoden Ihnen zu kompliziert und abstrakt erscheinen, ist es ratsam, sich an Fachspezialisten zu wenden. Diese Spezialisten haben das nötige Know-how und die Erfahrung, um komplexe Probleme aus Industrie und Forschung zu lösen und genaue Ergebnisse zu erzielen.







